作者：2018级本科生 程志刚 土木工程系

指导老师：陆新征 土木工程系

关键词：微震 LQR控制算法 深度学习 遗传算法

摘要

随着我国制造业高质量发展的推进，各企业对生产产品质量的要求也逐步提高，而周围环境的振动会对相关设备的使用及制造产生不利影响，有必要提出高效便捷的振动控制方法。尽管LQR控制算法可以控制大部分系统，但是由于LQR控制器参数固定，很难同时对不同振动类型的控制产生优异效果。本研究拟实现基于深度学习的振动识别，实现同时对多种类型的振动控制的优化。本研究首先收集被控系统工作空间中主要的振动信号，建立环境振动信号的数据库；经过初步处理后，对信号数据进行小波变换处理，通过遗传算法得到各类振动的最优控制参数；最后运用CNN、LSTM深度识别，匹配最优控制参数。之后展开案例分析，比较控制效果。

振动信号数据采集及预处理

采用加速度传感仪对工作环境中的典型振动进行采集，传感仪精度约10^-4g，满足振动干扰频率需求。为了测试复杂环境下的振动识别能力，主要振动源包括教学楼附近的基坑开挖施工引发的振动、学校周边交通及高铁运输引发的振动。

图1 时程数据信号

为便于后续参数调整，对振动信号进行预处理，切割并提取异常片段，统一信号长度为10s，因为信号的主要能量分布区间大致为10s左右。

振动对结构的作用不仅与信号的时域特性有关，还和其频域特征有密切关系。因此，对信号进行小波变换，对比不同类型振动在时频域的差异。如图所示为轻轨引起的振动信号的小波图，振动的小波能量在2~6s、2~8Hz范围内呈现较为明显的时频域集中特性，即具有低频特性。此外，通过小波处理得到的图像由于在合成图像的过程中可能会丢失部分特征，故同时提取小波系数矩阵。

图2 地铁振动时频域特征

LQR算法及最优控制参数确定

LQR算法控制效果由其关键参数QR系数矩阵决定，本研究采用遗传算法对不同类型振动输入下的LQR控制算法参数进行优化。控制对象案例选用单自由度结构，主要参数参考欧进萍的研究案例，并基于MATLAB进行仿真。

LQR经典振动控制算法中，通过设定系统的质量、刚度、阻尼比、自振频率等状态信息，对输入的振动信息响应，并同时进行主动控制，需要综合考虑控制效果和能量损失。因此对一定时间内的位移和控制力进行积分，得出损失函数，通过优化函数值而求解出最佳控制输出。

但是，算法中的Q、R矩阵则需要人为输入，而其带来的整体效果也会有所差异。因此，首先定义良好性能的度量标准，即兼顾效果与能量损失，设计出适应度函数，据此通过遗传算法多次随机选定参数，依据函数值输出最优Q、R矩阵。

深度学习振动识别

为实现较好的振动控制效果，需在尽可能短的时间内识别振动，但过短的振动信号会降低分类系统的识别精度，因此需要开展信号识别延时的参数分析。

对所有收集到的地铁与施工振动进行计算，设置不同的时间延迟，考虑振动与被控系统的卓越频率，以0.5s时间为间隔。振动控制效果则以前述遗传算法中的适应度函数进行评价，最后暂定1.5s延迟为相对最优延迟时间，需在振动的前1.5s内完成振动识别，选择最优参数。 

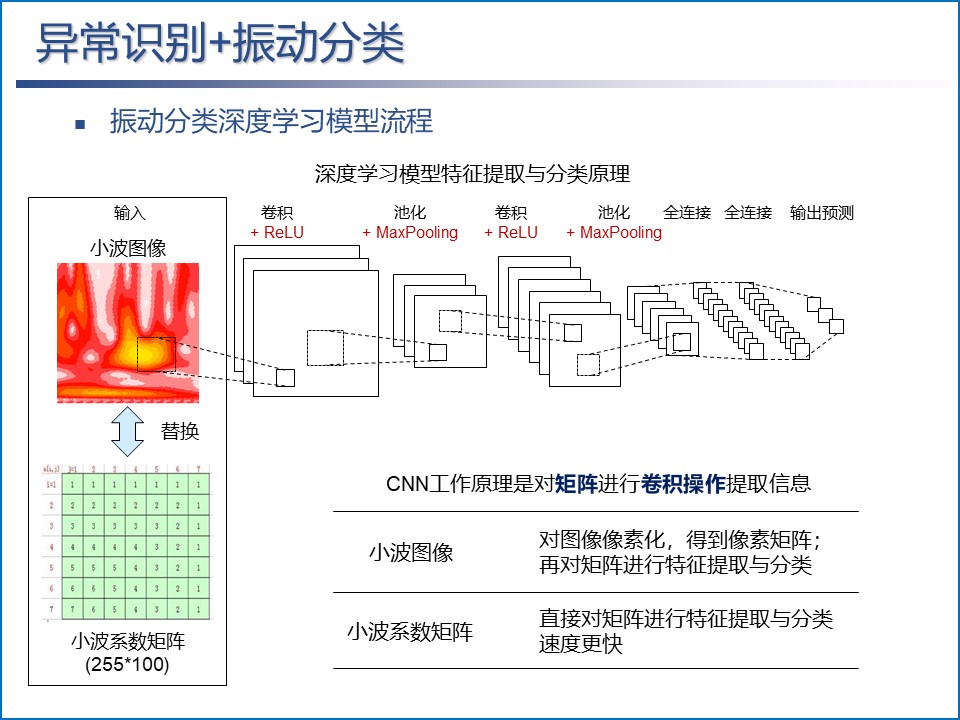
卷积神经网络（CNN）在图像识别领域应用广泛，图示为CNN的典型结构。CNN进行图像的特征提取时，会首先得到图像的像素矩阵。若以小波图作为输入则识别过程繁琐，包括：小波系数矩阵像素化为图像，被CNN前处理转化为矩阵。因此，在本研究中简化输入，其中一种输入为小波系数矩阵，另一种则为小波图。

图3 CNN网络架构

RNN 网络在不同时刻只有隐层单元 h 迭代，而在 LSTM 网络中，有两条迭代线路，一条和 RNN 网络一样，隐层单元 h，代表着网络架构最后的输出；同时另一条迭代线路 C，表示当前时刻 t 的记忆单元，通过输入门和遗忘门的信息选择进行迭代，最后跟随输出门，产生当前时刻的隐层单元状态。其输入参数与CNN网络输入相同，且分类标签暂时也相同，为输入数据的振动源代号。

图4 LSTM逻辑图

  最后，通过实际算例，混合多种数据，进行信号输入，随后比较识别效果，以及两种深度学习方法的处理效果。