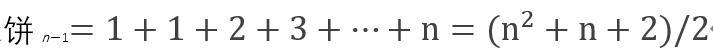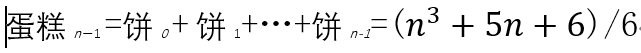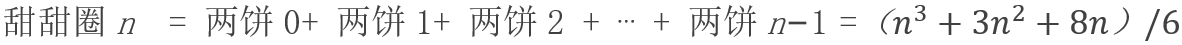作者：卜辰璟 所属院系 数学科学系

关键词：甜甜圈切块 几何

摘要

在甜甜圈上切两刀，最多能切成多少块？

这是一个有趣的问题，但是寻找答案的过程体现了解决数学问题的一般流程：通过直觉猜想出可能的方法和结果，再进行仔细论证。

切圆饼

甜甜圈是一个复杂的形状——它不仅是立体的，甚至还有一个洞。这对我们来说太难了。因此，我们先从简单的情况开始。考虑一个圆饼：

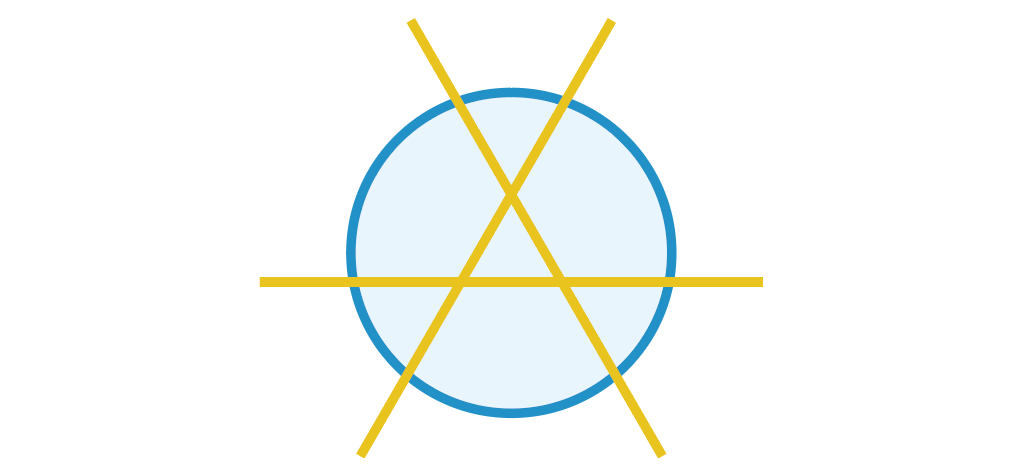
每切一刀，我们就把一些已有的块切成了两份。要知道切缝经过了多少个区域，只需要看它被已有的其它切缝分成了多少段。在切第n刀时，有n−1 条已有的缝。在最好的情况下，新的切缝与所有已有的切缝相交，形成n−1个交点，这些交点把新的切缝分成n段。因此，新增的块数最多是n。切n刀能把圆饼分成的块数最多是：

切蛋糕

考虑立体的图形。

每一刀都把一些已有的块切成两份。和之前不同的是，我们的第 3 刀的切面经过了 4 个已有的区域，把它们全都一分为二，得到 8 块蛋糕。事实上，要知道切面经过了多少个区域，只需要把这个切面单独拿出来看。我们发现，蛋糕的切面实际上是一个圆饼。新的切面和已有的切面相交于若干条直线，这就相当于在圆饼上切了若干刀。切第n刀时增加的块数最多是饼_n−1 。

例如，如果我们在蛋糕上切第 4 刀，可以这么切：

得到公式，在蛋糕上切n刀，得到的块数最多为：

切曲奇

接下来研究带洞的物体。曲奇上的洞可以看成是切了一刀，留下一个窄缝，但两端没有切断。把其两端切断，那么块数增加 2 块，这和在圆饼切n+ 1刀的情况一样，因此有曲奇_n = 饼_n+1 − 2 

切甜甜圈

   现在，我们做好准备，可以解决文章开头提出的问题。甜甜圈的本质是挖了一个洞的蛋糕。从曲奇和圆饼的联系可以猜测，甜甜圈和蛋糕也有类似的联系：甜甜圈n=蛋糕n+1−2，甜甜圈的洞可以看成蛋糕上切了一刀，但两端没有切断。如果切断的话，块数会多出 2。按照公式，预测两刀最多能把甜甜圈切6块；三刀，就能切成13 块；甜甜圈的切面可以是圆饼，曲奇或者两个圆饼。

饼n= (n2 + n + 2)/2 ，曲奇n = (n2 + 3n)/2 ，两饼n = (n2 + 3n + 4)/2 。切面是两个圆饼时，切面被分成的区域最多。因此，我们希望所有的切面都是两个圆饼。此时，总的块数最多是：