
作者:王天宇 清华大学经管学院
指导老师:王纯 清华大学经管学院
关键词:鲁棒优化 投资组合 条件期望风险
摘要
鲁棒优化方法广泛应用于资产组合优化,然而其参数选取往往对问题最优解有较大的影响。为合理估计不确定集参数以便减少保守程度,本研究使用分布式方法基于历史数据的聚类得到收益簇不确定集的信息,并利用统计性质选取参数进行优化,从而可将问题转化为易于求解的锥优化问题,与其他优化策略对比历史表现较好。进一步我们使用因子信息聚类构建情景决策树,使得本方法更具有解释性。
研究背景
最小化条件风险价值(CVaR)是现代最优投资组合选取的重要准则,如图1的一定概率水平下投资组合的期望损失。但实际仅从历史收益数据中直接估计均值-协方差优化样本外表现风险较高。分布式鲁棒优化即从数据中最差可能的参数分布出发,期望获得更好的样本外表现。但是这样基于最差分布的方法,结果过于保守。
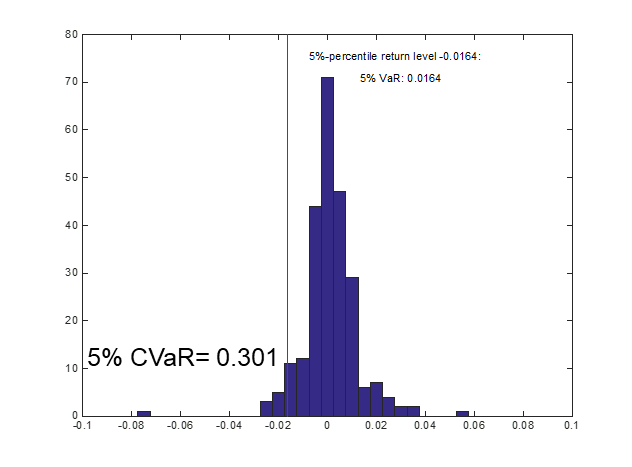
图1 实证情况的CVaR和VaR定义阐释
实际中我们采取的不同情况的决策树构建或是统计中聚类方法便是减弱保守程度。因此,这种情况下,我们便思考能否在多种情形下构建均值-协方差拓展原来单一的最差分布。
模型方法
通过历史收益来估计之前问题里的均值协方差,我们希望能够得到不同情况下的最差均值-协方差阵。因此我们构建了如下不同情形的模糊分布集:
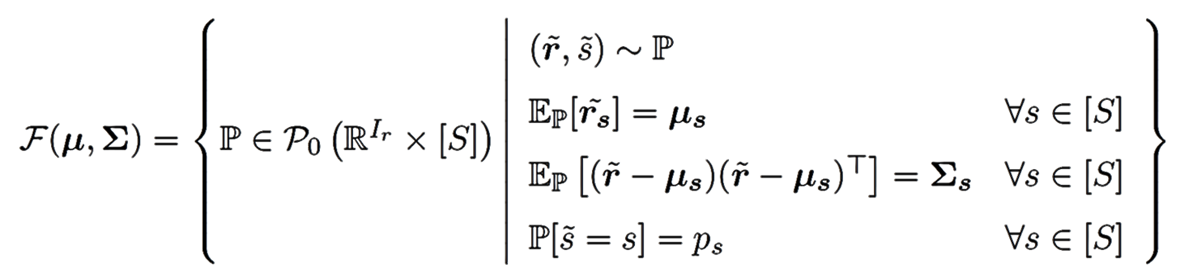
目标是从可能的最差分布下,最小化CVaR最优投资组合。给定这样的集合,该问题等价于下列一个锥优化的目标问题,能够保证计算执行性。
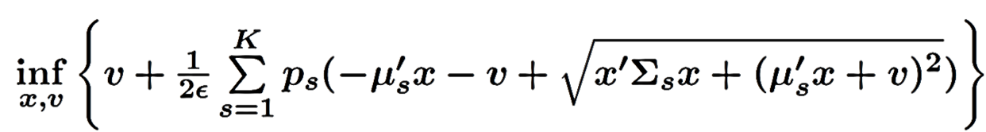
另一方面,针对这样多个簇的概率和矩信息,我们考虑其聚类方法的实现。一方面我们可直接由历史收益聚类,然后计算得到作为簇信息的参数;
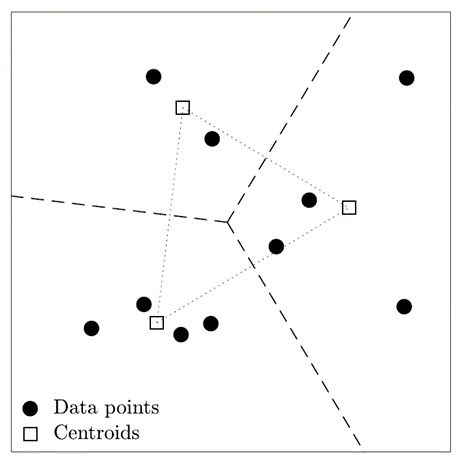
图2 基于直接聚类收益的方法阐释
另一方面由于市场信息更为稳定,我们选用因子模型如F-F 三因子/五因子等边际信息聚类得到每个簇的所有时间点,并因此投影计算到相应时间的收益聚类。后者的聚类计算量维数较低,但需要额外的边际信息。
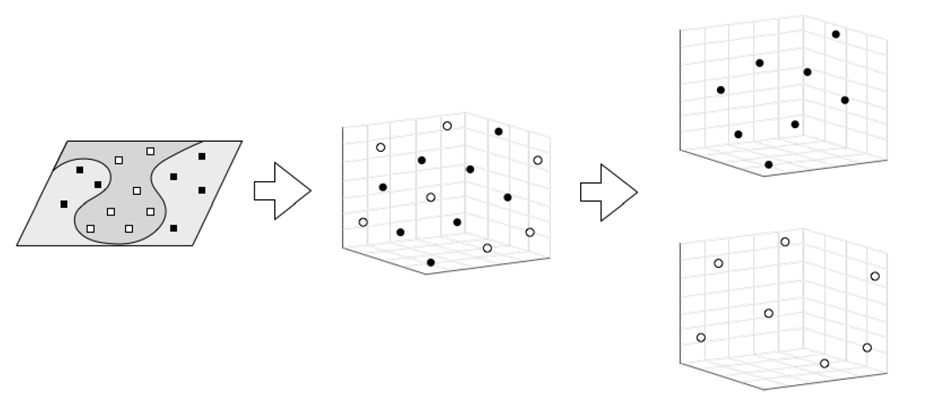
图3 基于因子边际信息的方法阐释
实证表现
我们在French网站上使用实际数据集上对方法进行了滚动窗口的测试,并选用其他基准策略与簇信息方法相比较。
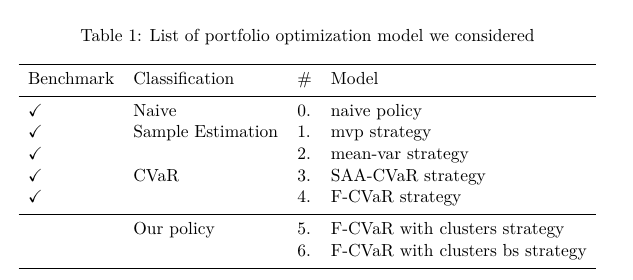
表1 实验中选取的不同策略的对比
在实际数据集中比较评价指标为:夏普比率,即同等风险下超额收益的量;实证的风险价值,如VaR / CVaR等;周转率,即每次投资组合变动的比率。以下是关于这些策略的比较结果:
表2 不同模型在评价指标上的实证表现
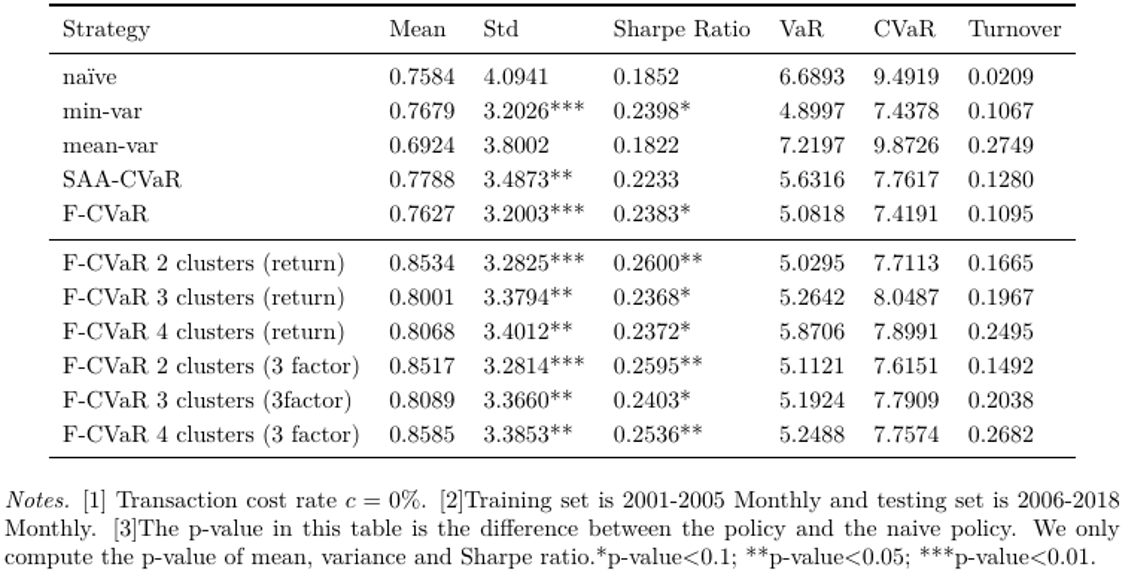
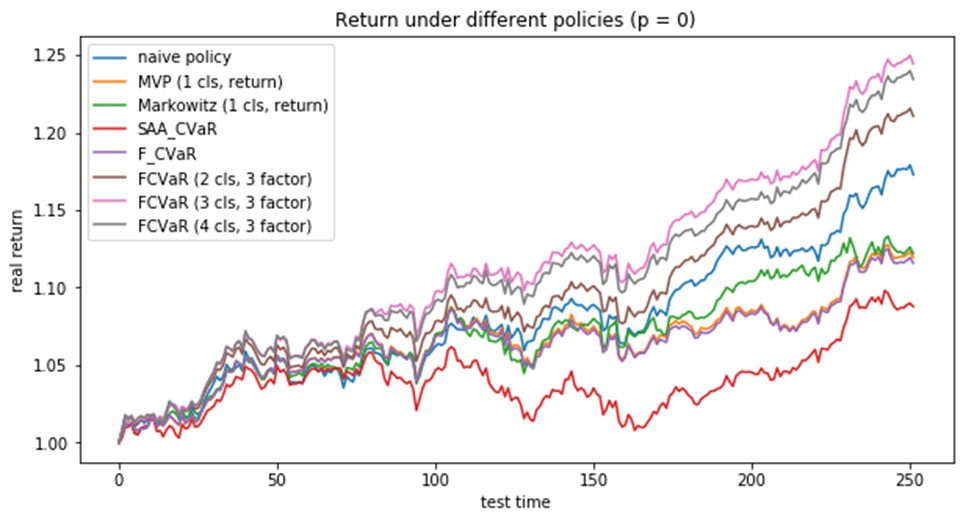
图1 不同模型在收益率上的实证表现
在与基准策略比较时,基于簇信息的方法会比目前的策略有明显的提升,表现在可以提高收益并减小方差,同时能控制使得风险价值变化不大。进一步地使用带有簇预测信息的规范性分析中,该模型仍然具有较好的表现。
表2 规范性分析的模型在评价指标上的实证表现

外部链接:
作者联系方式wangty.17@sem.tsinghua.edu.cn,
数据来源:
http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html






