
作者:2016级本科生 李沐恒 工程物理系
指导老师:应葵 工程物理学
关键词:核磁共振成像;磁共振温度成像;生物传热模型;Kalman滤波
摘要
磁共振温度成像能够为肿瘤热疗消融提供实时、全局的温度场监控,是保障消融安全、有效进行的重要技术手段。然而,临床中磁共振温度成像信噪比较低,这一现象在选用快速成像序列时尤为严重。针对这一问题,提出了基于Kalman滤波器和生物传热模型对磁共振温度成像进行滤波的方法。该方法将生物传热模型改写成Kalman滤波器中的状态转移矩阵形式,并将模拟温度和磁共振测温值相结合,以获得具有高精度和高信噪比的估计温度。临床仿真实验表明,该方法能将测温误差从6℃降至2℃;仿体实验表明,测量值与真实值的均方根误差值从1.927℃下降到0.735℃,且信噪比显著提升。
基于PRFS的磁共振测温
在磁共振成像过程中,多种参数均会随温度发生改变,从而衍生出一系列的测温方法。水质子共振相移与温度具有最好的线性关系。该方法的主要思想是在使用梯度回波序列采集数据的过程中,温度变化会导致采集图像的相位相较于基准图像发生线性变化。产生的相位变化和温度变化的关系可以描述为:

其中:ΔT表示温度变化,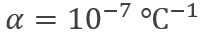 是比例系数,γ为旋磁比,B0是主磁场的磁感应强度,TE是回波时间。因此,在磁共振测温过程中,在已知初始温度T0时,实时测量的温度为:
是比例系数,γ为旋磁比,B0是主磁场的磁感应强度,TE是回波时间。因此,在磁共振测温过程中,在已知初始温度T0时,实时测量的温度为:
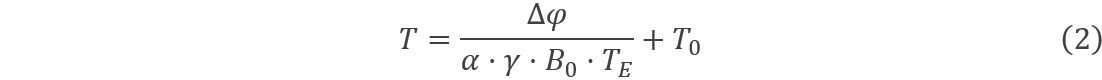
生物传热模型
生物传热模型的基础是Pennes于1948年提出的Pennes方程:

其中:ρ是组织密度,kg/m3;c是组织比热容,cb为血液比热容J/(kg℃);T为温度,℃;t为时间,s;λ是导热系数,W/(m·℃);Wb为毛细血管系统的灌注系数,kg/(m3·s);Tb为血液温度,在人体中认为温度恒为37℃;Q为热源项,W/m3。在实际仿真模拟中,为了提高计算效率,会将微血管组织灌注项并入导热系数项,视作等效导热系数,因而(3)式可以变为:
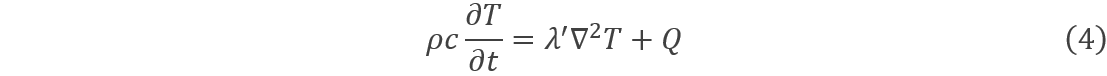
其中λ’是等效导热系数。考虑二维平面,将(4)式进行离散化处理,可以改写成差分形式,

式(5)中:下标i , j分别表示节点的坐标,上标则表示离散时间点。
Kalman滤波方法
Kalman 滤波器能够基于状态空间模型,从含噪声的观测数据中提取信号。在本文中,Kalman滤波器将利用生物传热模型模拟的温度和MRTI测量的温度,递推地估计出待测区域的实际温度。
Kalman滤波器的核心思想为:离散时间动态系统可通过描述状态向量的过程方程和描述观测向量的观测方程共同表示,通过对状态向量和观测向量进行线性组合,并求解使均方误差最小的加权矩阵,可以得到最终的估测向量。
将Kalman滤波方法运用到本问题中,生物传热模型对组织温度场的模拟过程可以视作状态转移过程,而通过MRTI方法对组织温度场测量的过程则可视作观测过程,利用相关算法即可计算得到实际温度场分布。

图1 生物传热模型与磁共振测温Kalman滤波算法

图2 数值仿真实验示意图
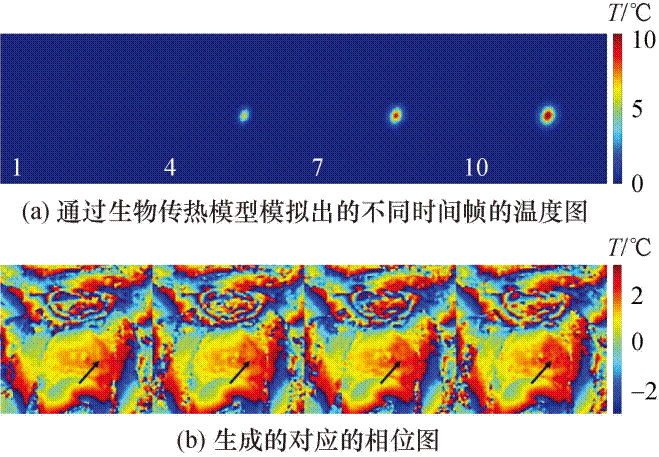
图3 相位模拟示意图

图4 仿体实验设计图

图5 临床仿真实验结果
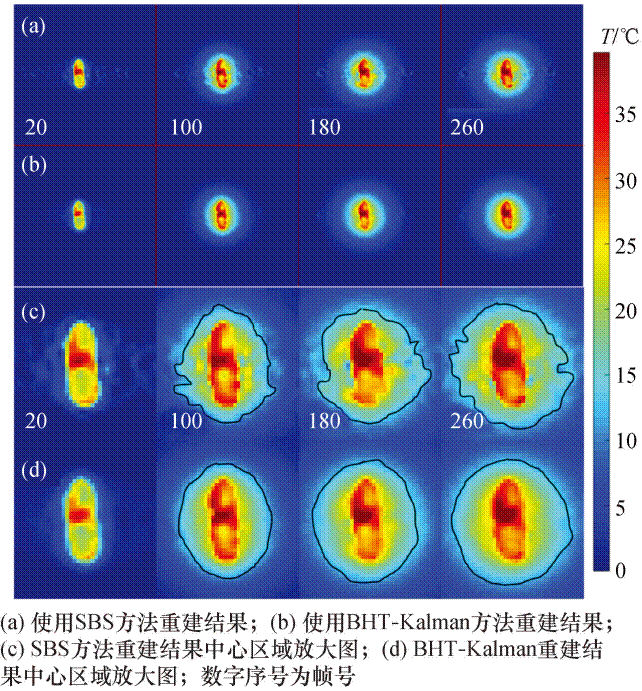
图6 仿真实验重建结果对比图

图7 仿体实验温度曲线






